November 30,2020 scientific research results | why students are biased by heuristics
The human brain always follows the principle of cognitive economy, that is to solve the problems in life to the greatest extent through the least cognitive efforts. Driven by this principle, heuristic thinking came into being. Heuristic thinking is a kind of fast cognitive process with little consumption of cognitive resources. It is a rule of thumb, which is a problem-solving strategy that depends on a great deal of experience. It can help us solve problems in most cases, but sometimes it will lead to deviation.
A typical heuristic strategy is to judge probability based on representativeness.For example “A The company has 100 Employees, of which 90 is a salesman, 10 is a programmer. Xiaoming is one of the A company's employees, he usually likes to read books related to mathematics and computer , he has high attainments in digital products such as computers and mobile phones, and usually likes to follow the tech-news. ”. In this description,many people would think that Xiaoming is a programmer on a large probability ,but ignored the basic probability of a salesman in the A company is actually much greater than a programmer.

Such heuristic thinking also exists in mathematics learning. Previous studies show,however,as students become familiar with proportionality, they tend to apply proportional reasoning in inappropriate situations , even if the situation of the problem is not proportional situation.This phenomenon,known as overuse of proportionality. For example, as in the following questions:
“ Xiaogang and Xiaohong are running around a track. They run equally fast but Xiaogang started later.When Xiaogang has run 3 laps, Xiaohong has run 9 laps.When Xiaogang completed 30 laps,how many laps has Xiaohong run? ”
Many students tend to interpret the covariation relation as proportionality and solve it by using“6×(9/3)=18”.But the problem should be solved in the way of“6+(9-3)=12 ”. This kind of wrong use of proportional reasoning exists in different cultural and educational environments, and it appears in the problem-solving of various mathematical fields, which shows that it is a systematic and widespread reasoning bias. Previous studies have found that this is because proportional reasoning is a heuristic strategy, which can be activated and used preferentially when solving the problem of co-variation. So how can students overcome this deviation? Professor Xiaodong Li's team recently published a paper in Cognitive Development.The paper systematically discusses the cognitive mechanism of this phenomenon.It has found that the heuristic bias is related to inhibition control and working memory capacity.
research findings
This studies designs a non symbolic Mathematical reasoning task (as shown in fig 1). The background of the mission is that two dwarfs are mining diamonds,each of them mine at a fixed speed. Their boss stops by erratically to check-in on their progress by counting the diamonds each dwarf has mined. The boss checks in on the dwarfs three times a day. Normally, the boss’s counts are correct; the boss’s assessment of the number of accumulated diamonds each dwarf mined for the first two checks is accurate. However, as the boss gets tired, he might make mistakes when counting the diamonds of the green draft during the last check-in. In the following task, the students need to figure out the numerical relationship between the diamonds minded by the yellow and the green dwarfs based on the totals from the first two check-ins, then evaluate whether the number of diamonds mined by the green dwarf (obtained during the last check-in) is correct.
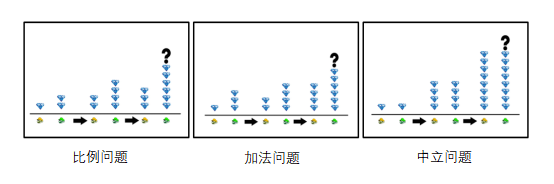
Fig.1. Samples of the three kinds of problem in the visual reasoning task
The task includes three types of problems:Proportion problem——The green dwarf mines diamonds N times faster than the yellow dwarfs , Addition problem —— The two dwarfs mine diamonds at the same speed, but the green dwarf mines N ahead of the yellow dwarf , Neutral question —— The two dwarfs mine diamonds at the same speed and start mining at the same time.
Firstly, the negative priming(NP) paradigm is used to verify whether students need to suppress proportional reasoning when solving non proportion problems (addition problems). The logic of the NP paradigm is as follow: If a heuristic strategy is inhibited in a prior task, then the subsequent processing of that strategy will be impaired, and the impairment is typically indicated by a slower or less accurate response.According to this logic, two conditions were designed in the experiment. Under the test condition, the students were asked to solve an addition problem and then a proportion problem, while under the control condition, the students were asked to solve a neutral problem first and then a proportion problem (Fig 2)。
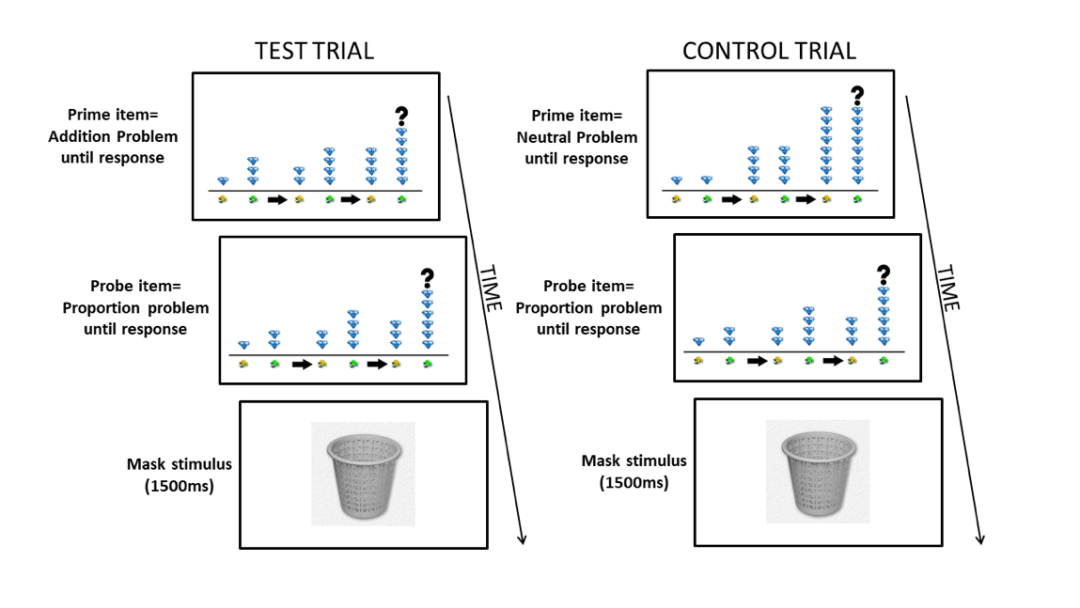
Fig.2. Procedures for test trials and control trials
As the neutral problem only needs to compare whether the number of diamonds is the same or not, there is no need to use addition or proportion strategy, which will not affect the following proportion problem. Therefore, if students need to suppress proportional reasoning in solving the addition problems, the students' performance in solving the proportion problem under the test condition will be worse than that under the control condition. The results showed that the reaction time of the students to solve the proportion problem after solving the addition problem did become longer, and there was a negative priming effect, so the hypothesis that the students need to restrain proportional reasoning is verified 。
However, the negative priming effect can only show that the students need to restrain proportional reasoning to solve non proportional problems successfully, but it can not explain whether the reason why students overuse proportional reasoning is that they do not realize the conflict between problem-solving strategies and problem situations, or they are aware of the conflicts but can not effectively suppress the misleading of this heuristic strategy?
In order to verify this problem, the studies adopts the paradigm of self-confidence detection (Fig 3 )The task asked students to indicate how confident they were about their response to two reasoning problems.The logic of the paradigm is that if the students can detect the conflicts, their confidence in the correctness of their answers will decrease when they use heuristic incorrectly compared with the case of correct answers.
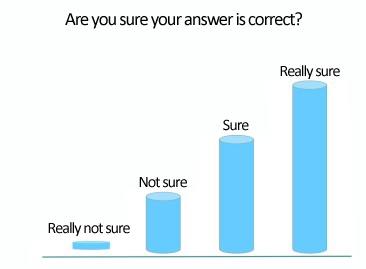
Fig.3.The 4-point confidence rating scale
The experimental results show that, compared with the correct use of the strategy( Group2 ), after the students mistakenly used proportional reasoning to solve the addition problems( Group1 ), the self-confidence is decreased significantly.It is explain that the student is not “ Happy fool ” ,they can still realize that it is not right to use proportional reasoning to solve the problem of addition, but they can't suppress the impulse to use proportional reasoning.
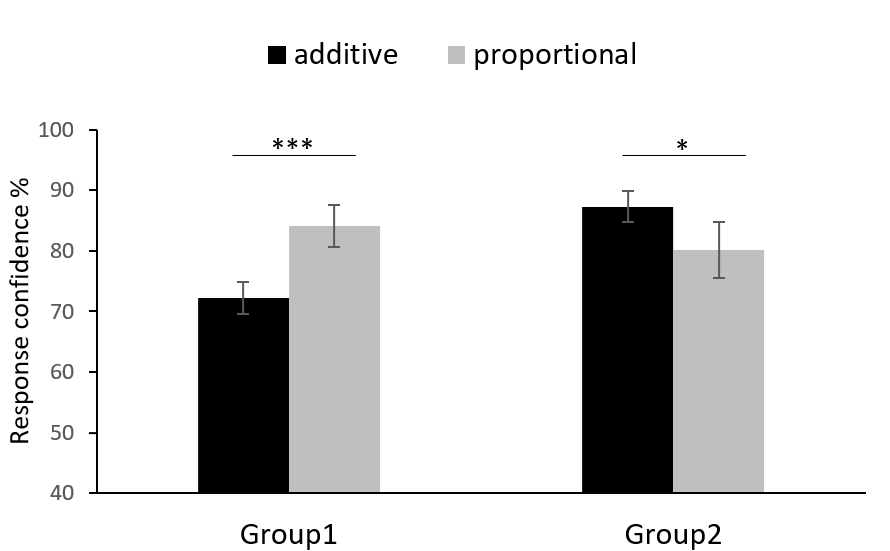
Fig.4. Comparison of self-confidence between the overuse of proportional inference group( Group1 )and the correct problem solving group( Group2 )in addition problem and proportion problem.
Finally, the paper discusses the relationship between working memory span and inhibition heuristic bias. The experiment use the visual spatial working memory span task (Fig 5)to measure the working memory span of students. The results showed that the scores of working memory are significantly negatively correlated with the error rate of addition problems in negative priming paradigm and proportion problems under test conditions, indicating that the performance of inhibition control is related to working memory.
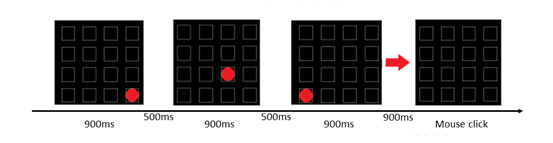
Fig. 5. A sample trial of the VSWM task. Each stimulus was presented for 900 ms; the interval of each stimulus was 500 ms, and there was a 900 ms interval between the stimuli and the recall test.
In general, this study shows that students will be affected by heuristic bias in the process of mathematics learning, and overcoming this deviation requires the participation of inhibition control, and working memory span provides support for inhibition control. This finding helps educators to understand the systematic errors of students in the learning process, and provides a new idea for promoting the mathematics learning of primary and secondary school students. Future education should pay more attention to the role of executive function in learning.
Paper details
Cognitive Development is a JCR 2 area magazine in the field of SSCI development psychology. Dr. Ronghuan Jiang and Professor Xiaodong Li are the first authors of this paper, and Professor Xiaodong Li is the corresponding author. This research is a phased research achievement of "Experimental Research on cognitive inhibition and mathematical problem solving" supported by National Social Science Foundation.
References:
Jiang, R., Li, X., Xu, P., & Mao, T. (2020). Why students are biased by heuristics: examining the role of inhibitory control, conflict detection, and working memory in the case of overusing proportionality. Cognitive Development, 53, 100850. https://doi.org/10.1016/j.cogdev.2020.100850

 WeChat
WeChat